第一题:某反应器容积为1.213m3,内装有温度为227℃的乙醇45.40kg。现请你试用以下三种方法求取该反应器的压力,并与实验值(2.75MPa)比较误差。(1)用理想气体方程;(2)用RK方程;(3)用普遍化状态方程。
解:
乙醇的相对分子质量为46.07kg/kmol,则乙醇的摩尔数为
n=45.40/46.07=0.9854kmol
乙醇的摩尔体积为:
V=V总/n=1.213/0.9854=1.2309 m3/kmol
温度T=227+273=500K
(1)理想气体方程

误差=(3.377-2.75)/2.75=22.8%
(2)用RK方程
从附录2查得乙醇的临界参数为:
Tc=516.2K pc=6.383 MPa ω=0.635 Vc=167 cm3/mol
首先,计算RK方程参数a和b:
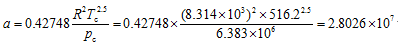
Pa.m6.K0.5.kmol-2
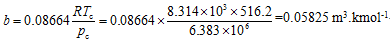
然后,直接代入RK方程,则
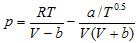
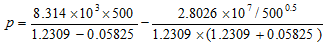
p=2.755×106Pa=2.755MPa
误差=(2.755-2.75)/2.75=0.18%
(3)用普遍化状态方程
首先判断使用范围:
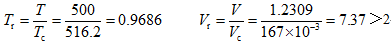
所以可以采用普遍化第二virial系数法计算。
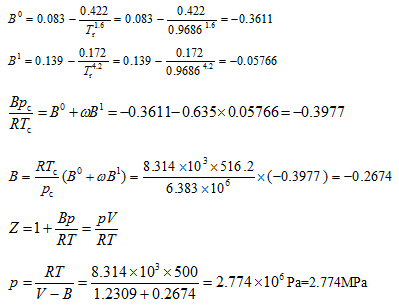
误差=(2.774-2.75)/2.75=0.87 %
说明:理想气体方程误差最大;RK方程误差最小;普遍化方法居中。
n=45.40/46.07=0.9854kmol
乙醇的摩尔体积为:
V=V总/n=1.213/0.9854=1.2309 m3/kmol
温度T=227+273=500K
(1)理想气体方程
误差=(3.377-2.75)/2.75=22.8%
(2)用RK方程
从附录2查得乙醇的临界参数为:
Tc=516.2K pc=6.383 MPa ω=0.635 Vc=167 cm3/mol
首先,计算RK方程参数a和b:
Pa.m6.K0.5.kmol-2
然后,直接代入RK方程,则
p=2.755×106Pa=2.755MPa
误差=(2.755-2.75)/2.75=0.18%
(3)用普遍化状态方程
首先判断使用范围:
所以可以采用普遍化第二virial系数法计算。
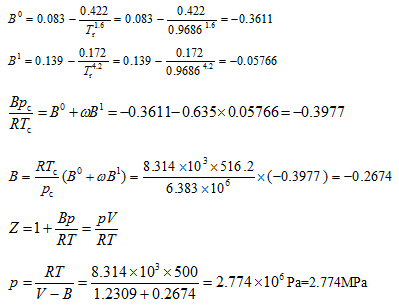
误差=(2.774-2.75)/2.75=0.87 %
说明:理想气体方程误差最大;RK方程误差最小;普遍化方法居中。
注意:
① 状态方程中V是摩尔体积,不是体积;
② 在判断普遍化方法时,由于压力p未知,故用对比体积判断。
③ 用普遍化第二virial系数法计算压力p时,不需要试差,将二项virial截断式进行变换即可。
① 状态方程中V是摩尔体积,不是体积;
② 在判断普遍化方法时,由于压力p未知,故用对比体积判断。
③ 用普遍化第二virial系数法计算压力p时,不需要试差,将二项virial截断式进行变换即可。
第二题:一个0.5m3压力容器,其极限压力为2.75MPa,若许用压力为极限压力的一半,试用普遍化第二virial系数法计算该容器在130℃时,最多能装入多少丙烷?已知:丙烷Tc=369.85K,pc=4.249 MPa,ω=0.152 。
解:
已知T=130+273=403K,p=2.75/2=1.375MPa
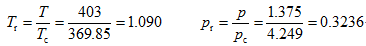
查图2-14可知该点位于曲线之上,可用普遍化第二virial系数法计算。
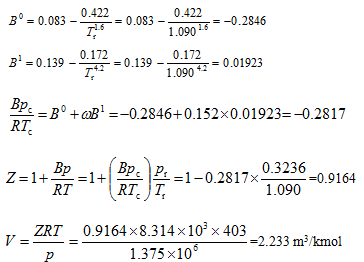
丙烷的摩尔数为n=0.5/2.233=0.2239 kmol
丙烷的质量=0.2239×44.10=9.87 kg (相对分子质量: 44.10 kg/kmol)
即最多能装入丙烷9.87 kg
查图2-14可知该点位于曲线之上,可用普遍化第二virial系数法计算。
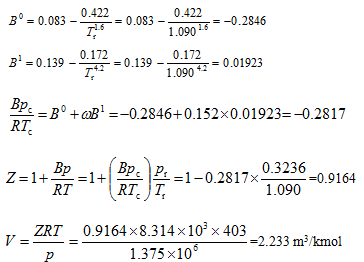
丙烷的摩尔数为n=0.5/2.233=0.2239 kmol
丙烷的质量=0.2239×44.10=9.87 kg (相对分子质量: 44.10 kg/kmol)
即最多能装入丙烷9.87 kg
注意:
① 在用普遍化第二virial系数法计算时,需要判断已知条件的使用范围是否符合方法的适用条件。
② 计算物质的量,应是可以直接计量的量,如质量,体积等,所以本题计算出摩尔数后应换算成质量。
① 在用普遍化第二virial系数法计算时,需要判断已知条件的使用范围是否符合方法的适用条件。
② 计算物质的量,应是可以直接计量的量,如质量,体积等,所以本题计算出摩尔数后应换算成质量。

